Month: May 2016

Fortsätter från tidigare inlägg om rummen (F,T) och (W,T). Tänkte framför allt hålla mig till (F,T) den här gången.

Vi har slagit fast att (F,T) är ett metriskt rum. Nu tänkte jag skapa ett mått på rummet, så att det blir ett måttrum. Målet med måttet är att mäta hur “sammankopplade” olika grupper av människor är.

Jag börjar med att gå tillbaka till det tidigare definierade länk-predikatet. Två element (personer) i (F,T) är länkade ifall det går att koppla samman dem genom vänskapsrelationer på Facebook. Värdet på länken är antalet personer som den går igenom. Sen definierades d(a,b) som inf{L | L är länk(a,b)}.

För att kunna definiera ett mått behöver vi en så kallad sigma-algebra, vars element måttet definieras för. I detta fallet består min sigma-algebra A av alla underrum (subspace) till (F,T).

För att kontrollera ifall A verkligen är en sigma-algebra kontrollerar vi följande:

(i) att F är i A.
(ii) att ifall B är i A, så är komplementet (F B) i A.
(iii) att unionen av en uppräknelig mängd B i A också är i A.

Alla tre axiom uppfylls trivialt av A, eftersom A är mängden av alla underrum till (F,T).

Nästa steg är att definiera själva måttet. Jag börjar med att definiera vad jag kallar en storlek av en boll i (F,T); storleken av Bd(x,ε) är antalet punkter inuti Bd(x,ε).

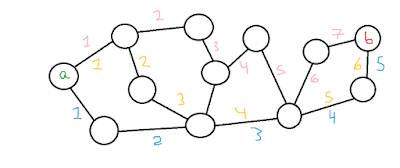
Jag definierar μ(B) som summan av storleken av de största bollar man kan skapa runt varje punkt i B, så att bollen bara innehåller punkter i B. Se bilden nedan för exempel på vad jag menar.

Här ser vi tre av de granskade bollarna – Bd(b1,1), Bd(b2,2), Bd(b3,3)

Då blir alltså μ(B) = ΣbϵB(sup{storlek Bd(b,ε) | ∀xϵBd(b,ε) xϵB}).

I exemplet på bilden så blir μ(B) = 1 + 3 + 11 + 11 + 8 + 3 + 3 + 4 + 5 + 1 + 3 + 1 + 1 = 55, vilket är vårt mått på hur sammankopplad B är.

För att undersöka så att μ är ett väldefinierat mått kollar vi axiomen:

(i) μ(B) ≥ 0
(ii) μ(∅) = 0
(iii) μ av en uppräknelig union av disjunkta mängder är samma som summan av μ av varje mängd.

Att (i) stämmer för vårt mått följer av att den minsta mängd som innehåller ett element har måttet 1, eftersom vi då kan konstruera en boll runt det elementet.

Att (ii) stämmer följer av att den enda boll vi kan konstruera runt ett element i ∅, så att alla element i bollen är i ∅, är den tomma bollen.

Att (iii) stämmer inses snabbt, då måttet av A inte är beroende av måttet för B, ifall A och B är disjunkta.

Med hjälp av det här måttet kan vi som sagt mäta hur pass väl sammankopplad en grupp människor på Facebook är.

Är olika rum på webben topologier? Jag föreställer mig framför allt två stycken rum till att börja med – rummet av personer och vänskapsrelationer på Facebook; och rummet av artiklar och hyperlänkar på Wikipedia.

Låt oss definiera avståndet mellan två personer a och b på Facebook med grund i konceptet “länk”. Vi definierar detta predikat genom att x och y är “länkade” ifall det går att koppla samman dem genom vänskapsrelationer (så att t.ex. x är vän med z som är vän med t som är vän med y). Värdet på den här länken är antalet vänskapsrelationer som är involverade (i exemplet alltså 3). Vi definierar avståndet från a till b som den länk mellan dem med lägst värde.

Här ser vi tre olika länkar mellan a och b. Den blå länken har värde 5, den rosa värde 7 och den orangea värde 6.

Så d(a,b) = inf{L | L är länk(a,b)}.

Är detta en väldefinierad metrik (metric) på rummet av personer på Facebook?

(i) d(a,b) = inf{L | L är länk(a,b)} = inf{L | L är länk(b,a)} = d(b,a)

(ii) d(a,b) kan inte vara lägre än noll, då inf{L | L är länk(a,b)} är antalet vänskapsrelationer för att komma från a till b – detta kan inte vara negativt.

(iii) d(a,b) = 0 endast om a och b är samma person; annars krävs det minst en vänskapsrelation för att komma från a till b.

(iv) Om d(a,b) = inf{länk(a,b)} = x, så är d(a,c) + d(c,b) = inf{L | L är länk(a,c)}+inf{L | L är länk(c,b)}, vilket som lägst kan vara x; det är det då c ingår i den länk mellan a och b som har lägst värde, dvs ifall c är en av de personer vars vänskaper ingår i kedjan. Om c inte är en av de personerna, så måste vägen från a till b via c vara längre än den kortaste vägen mellan a och b, så att d(a,b) ≤ d(a,c)+d(c,b).

Vi ser att d(a,c)+d(c,b) bara är samma som d(a,b) ifall den streckade relationen finns, annars är d(a,b) mindre.

Då vet vi att d är en väldefinierad metrik.

Utifrån d kan vi sedan på standardmanér inducera en topologi T på rummet av Facebook-personer F, med bas-element av formen Bd(x,ε) – dvs mängden av alla personer vars avstånd till x definierat genom d är mindre än ε.

Här ser vi den röda mängden av alla personer inom avståndet 3 från x, och den blå mängden av alla personer inom avståndet 2 från y.

Hur ser då rummet (F,T) ut?

Eftersom (F,T) är ett metriskt rum så är kompakthet samma sak som sekvenskompakthet (sequentially compact), så ifall varje oändlig sekvens i (F,T) innehåller en konvergent undersekvens (subsequence), så är rummet kompakt. Detta verkar trivialt sant för mig, då mängden användare på Facebook är ändlig, så en oändlig sekvens i (F,T) måste innehålla någon person en oändlig mängd gånger; definiera dessa som den konvergenta undersekvensen.

Ifall (F,T) är sammanhängande (connected) eller inte tror jag inte att jag kan svara på utan en djupare undersökning av hur rummet faktiskt ser ut. Vad jag kan konstatera är att det åtminstone kan finnas delmängder som inte är sammanhängande. Se bilden nedan.

A delas upp i Bd(y,3) och Bd(x,3)

Detta kan ontologiskt förstås som att gruppen av människor i A kan delas in i två stycken kretsar eller sociala grupper, nämligen Bd(y,3) och Bd(x,3).

På liknande manér kan man föreställa sig rummet av artiklar på Wikipedia – W – och den metrik som skapas genom att titta på hyperlänkskedjor mellan artiklarna.

Definiera avståndet mellan två artiklar a och b i W genom att d(a,b) = inf{länkkedja(a,b)}, där en länkkedja är en “väg” av hyperlänkar inom W från a till b, och värdet på länkkedjan är antalet sådana hyperlänkar som används. Avståndet är alltså så många hyperlänkar inom W som krävs för att komma från a till b på snabbast vis.

Är detta en väldefinierad metrik på W?

Ja, enligt samma argumentation som med F.

Så vi har ett till topologiskt rum, nämligen (W,T), med topologi inducerad från metriken ovan.

Med dessa topologier som grund kan vi undersöka hur de rummen jag intresserar mig för ser ut. Jag intresserar mig främst för två frågor, initialt:

1. Kan man genom att undersöka (F,T) se ifall de traditionella indelningarna av samhället (t.ex. klassindelningar) speglas i (F,T), eller om man kanske måste uppdatera vilka sociala grupperingar som används i t.ex. sociologisk forskning?

2. Kan man genom att undersöka (W,T) se ifall olika ämnen som traditionellt separeras på akademin är lika separerade i (W,T) som på akademin, eller ifall tvärvetenskapligheten redan är ett faktum?

George Berkely lade fram en ontologisk princip i sin idealistiska filosofi – esse est percipi. Existensen för de fysiska objekten utgörs av dess egenskap av att iakttas – “existence consists in being perceived“. För att förtydliga: Berkeley menar inte (vad jag förstått) att ett ting, så att säga, ges tillåtelse att existera av det faktum att det iaktas – utan att ett tings själva existens utgörs av dess iakttagenhet. Denna ontologiska princip har sedan dess förkastats av många filosofer på grund av bland annat dess paradoxala konsekvenser kring ting som glider in och ut ur existensen (föreställ dig en penna som du lägger i en byrålåda som du sedan stänger; tror du verkligen att pennan slutat finnas då, och att den sedan “återuppstår” när du öppnar lådan igen?).

Men jag vill hävda att Berkeleys filosofi kan få djupare konsekvenser om man nyttjar den för att betrakta vår moderna existens. Esse est percipi är nämligen den princip som ligger bakom det snart allomfattande kravet på en närvaro vid Facebooks “sociala” plattform.

“Deltagandet har fått mer och mer av plikt över sig. Man känner att man måste logga in för att upprätthålla kontakter med släktingar, för att inte missa viktiga tillställningar, för att få jobb, för att kunna nå ut med sina egna arrangemang. Flödet börjar likna ett löpande band.” 

Man kan säga att det finns en disciplinerande aspekt av närvaron på Facebook. Facebook är uppbyggt som så att den som är aktiv syns och den som är inaktiv sållas bort i människors flöde – i den nya webblogikens “fönster” till internet. Inte bara för företags sidor och hobbymusikers fangrupper, utan även för de privatpersoner som söker den vardagliga bekräftelsen i “like”-knappen. Gilla-knappen driver fram en existentiell kris när humana kvalitéer ska kvantifieras och mätas (och säljas); samma faktor syns här som i humaniorans svenska kris.

““I’m on it nonstop, like nonstop, like 20 hours a day,” says Courtney, the one who looks like a 70s movie star.  “It’s, like, fun to get the messages,” Danielle says. “If someone ‘likes’ you, they think you’re attractive.”  “It’s a confidence booster,” says Jessica, 21, the one who looks like a Swedish tennis player.”

Eftersom du existerar endast om du iakttages och du bara lyfts fram för iakttagande om du ger Facebooks algoritmer vad de vill ha, så disciplineras du till exhibitionism av existensiella skäl. Långsamt inlärs ett beteende genom pavlovsk stimulation där bilder på ens barn som äter fläks ut till snart sagt hela världen, blandade med rop på hjälp i mörka stunder och bekräftande av att man gillar Harry Potter. Genom att exponera sitt privatliv på detta vis så bekräftas man som person – man ges existens. Esse est percipi har blivit en existensiell princip, snarare än ontologisk.

Denna exhibitionism är vad som driver profiten hos den privata övervakningsindustrin – Facebook, Twitter, Snapchat, Google, Spotify, snart sagt alla uppseglande så kallade “IT-under” – de där som ska driva den svenska ekonomin och skapa de nya jobben (med andra ord den nya Messias-gestalten) – tjänar sina pengar genom att psykologiskt driva fram detaljer om vårt privatliv för att sedan sälja det vidare.

Vi bygger frivilligt det ultimata Panopticon, i Jeremy Benthams ord:

“[A] new mode of obtaining power of mind over mind, in a quantity hitherto without example.”

Eller som Wikipedia beskriver det:

“The concept of the design is to allow all (pan-) inmates of an institution to be observed (-opticon) by a single watchman without the inmates being able to tell whether or not they are being watched.”

Inte bara har vi mer eller mindre utan motstånd gett upp vårt privatliv till företag för att sälja vidare och tjäna pengar på, men i symbios med dessa företag finns den statliga övervakningsindustrin. Tack vare vår framdrivna, existentiella exhibitionism har stater världen över (främst USA, dock) bättre insyn i våra liv än någon sin förr. Den problematiska pseudonymiteten som dominerade det tidiga internet ger vika för det Panopticon som inte kan respektera en individs möjlighet att uttrycka sig utan dess närvaro och registrering.